9 logiske opgaver, at tænderne kun intellektuelle
Danner Uddannelsesprogram / / December 19, 2019
1. Fødselsdag Cheryl
Antag nogle Bernard og Albert nylig mødtes med pigen Cheryl. De ønsker at vide, hvornår hendes fødselsdag - at forberede gaver. Men Cheryl er det mere lille ting. I stedet for svar, hun giver fyrene en liste over 10 mulige datoer:
| 15. maj | maj 16 | maj 19 |
| 17th juni | 18 juni | |
| 14th juli | 16th juli | |
| 14 august | 15th august | 17th august |
Forudsigeligt opdaget, at den unge mand ikke kan beregne den korrekte dato Cheryl hvisken i hans øre, Albert kalder kun en måned af hendes fødsel. Og Bernard - også stille - blot et tal.
- Hmm, - siger Albert. - Jeg ved ikke, hvornår Cheryl fødselsdag. Men jeg ved, at Bernhard ikke kender dette.
- Ha - opfylder Bernard. - I første omgang vidste jeg ikke, da Cheryl fødselsdag, men nu ved jeg det!
- Ja, - er enig Albert. - Nu ved jeg, at også.
Og de kaldte i kor bestemt dato. Da Cheryl fødselsdag?
Hvis du ikke er i stand til at gå for at finde svaret, så fortvivl ikke. For første gang denne spørgsmål blev stillet i teenage Matematisk Olympiade i SingaporeSingapore og asiatiske School Math Olympiade
Hvilket er berømt for de højeste uddannelsesmæssige standarder. Når en af de lokale oplægsholdere offentliggjort i denne skærm puslespil til Facebook, blev det viraleHvornår er Cheryl fødselsdag? 'Den vanskelige matematik problem, der har alle forvirrede: Løs den forsøgte at titusinder af brugere af Facebook, Twitter, Reddit. Men alle har fejlet.Vi er overbeviste om, at du får. Otgadku ikke åbnes, før i det mindste ikke prøve.
Se svaret.
Skjul.
Juli 16th. Dette følger af den dialog, der fandt sted mellem Albert og Bernard. Plus en lille udelukkelsesmetoden. See.
Hvis Cheryl blev født i maj eller juni, så hendes fødselsdag kan være det 19. eller 18.. Disse tal er fundet i kun én gang listen. Derfor Bernard, høre dem, bare kunne se om et pågældende måned. Men Albert, som følger af dens første kopi, jeg er sikker på, Bernard, vel vidende nummeret, absolut ikke vil være i stand til at ringe til en måned. Så taler vi ikke om maj eller juni. Cheryl blev født i den måned, hver af disse datoer, hvor der er en dobbelt i de tilstødende måneder. Det er - i juli eller august.
Bernard, hvem ved fødslen, hørelse og analysere replika Albert (der er, at finde ud af om juli eller august), siger, at nu kender det korrekte svar. Heraf følger, at et vist antal Bernardo - ikke 14, fordi det er duplikeret, og i juli og august, så det er umuligt at bestemme den korrekte dato. Men Bernard sikker i sin beslutning. Så betyder det antal kendte ham ikke dobbelt i juli og august. Under denne betingelse få tre muligheder: 16 juli, 15. august og 17. august.
Til gengæld Albert hørte ordene fra Bernard (og logisk, før de når de ovennævnte tre mulige datoer), erklærede, at nu også kender den korrekte dato. Vi husker, at Albert er kendt for en måned. Hvis denne måned var August, kunne den unge mand ikke bestemme antallet af - faktisk i august featured blot to. Så er der kun én mulighed - 16 juli.
2. Hvor gamle døtre
På gaden en dag, to tidligere klassekammerater mødtes og havde en dialog mellem dem.
- Hej!
- Hej!
- Hvordan har du det?
- Godt. Grow to døtre, doshkolnitsy mere.
- Og hvor gamle er de?
- godt ved... produktet af deres alder er lig med antallet af duer på vores fødder.
- Disse oplysninger er ikke nok for mig!
- senior ligesom sin mor.
- Nu ved jeg, at svaret på dit spørgsmål!
Så hvor mange år døtre en af de samtalepartnere?
Se svaret.
Skjul.
1 og 4 år. Da svaret blev klart efter at have modtaget information, som en af de døtre af ældre, så før der var tvetydighed. I første omgang, baseret på antallet af duer, den variant, der døtre - tvillinger (det vil sige, deres alder er ens). Dette er kun muligt med antallet af duer er de firkantede tal op til og med 7 (7 år - den alder, hvor børnene går i skole, det er, ophører med at være førskolebørn): 1, 4, 9, 16, 25, 36, 49.
Ud fra disse kvadrater, kan kun én opnås ved multiplikation af to forskellige numre, som hver især er lig med eller mindre end 7, 4 - (1 × 4). Følgelig døtre 1 og 4 år. Andre hel mens "pre" Der er ikke noget alternativ.
3. Hvor er min bil?!
De siger at problemet er givet ved de studerende på junior klasser af Hongkong skoler. Børn beslutter det er bogstaveligt talt i sekunder.
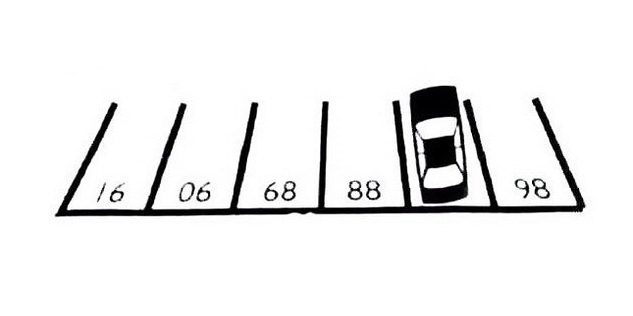
Navngiv antal parkeringspladser, som tager bilen.
Se svaret.
Skjul.
87. For at gætte, bare se på billedet på den anden side. Så de numre, du ser nu på hovedet, tage den rette position - 86, 87, 88, 89, 90, 91.
4. Kærlighed i Kleptopii
Jan og Maria elsker hinanden, kommunikerer via internettet. Jan vil sende Mary en vielsesring med posten - til give et tilbud. Men her er det springende punkt: elskede land bor i Kleptopii hvor en parcel transmitteret via mail, er forpligtet til at være stjålet - hvis den ikke er lukket inde i en kasse med en lås.
Hos John og Marys mange slotte, men sende hinanden nøgler, kan de ikke - fordi tasterne også vil være stjålet. Hvordan til at sende Jan ring til det helt sikkert har fået i hænderne på Mary?
Se svaret.
Skjul.
Yang bør sende Maria en ring i et aflåst boks. Uden nøglen, selvfølgelig. Maria modtog pakken, bør indgå i hendes eget slot.
Så Jan sendt en kasse igen. Han åbnede sine egen nøgle og lås re-adresser pakken med den eneste tilbageværende låst lås Mary. Og pigen er nøglen til det.
I øvrigt, denne opgave - ikke bare en teoretisk spil logik. Anvendes i sin idé - en fundamentalSyv Puslespil du tror du må ikke have Heard korrekt Key Exchange kryptografisk princip om Protokol Diffie - Hellman. Denne protokol giver to eller flere parter for at få den delte hemmelige nøgle over en usikker kommunikationskanal lytning.
5. På jagt efter dokumentfalsk
Den kurer bragte dig 10 poser, hver med en masse mønter. Og alle ville være godt, men du har mistanke om, at pengene i en af de falske poser. Alt hvad du ved med sikkerhed - det er hvad ægte mønter vejer 1 g hver, og falsk - 1,1 g Andre forskelle mellem de penge der.
Heldigvis har du en nøjagtig digital skala, der viser vægten af op til en tiendedel gram. Men kurer i en fart.
Kort sagt, nej, får du kun én forsøg på at bruge vægte. Ifølge et vejer præcist beregne i hvilken en pose er falske mønter og om der er sådan en taske i det hele?
Se svaret.
Skjul.
Et vejer nok. Bare sætte på skalaerne bare 55 mønter: 1 - fra den første pose, 2 - i den anden, 3 - i den tredje, fire - fra den fjerde... 10 - fra den tiende. Hvis hele masse penge vil veje 55 g - så falsk ikke er i en af poserne. Men hvis vægten vil være anderledes, vil du straks forstå, hvad serienummeret på poser fulde af forfalskninger.
Overvej om angivelser af vægte vil adskille sig fra referencenumre 0,1 - falske mønter i den første pose, 0,2 - i andet, 0,3 - i den tredje... 1.0 - en tiendedel.
6. haler ligestilling
I den mørke-mørke (nu ikke se nogen DIG, og du kan ikke tænde lyset), rummet er et bord, hvorpå er 50 mønter. Du behøver ikke se dem, men du kan røre, flip. Og vigtigst af alt, vide præcis: 40 mønter oprindeligt ligger ørn op, og 10 - haler.
Din opgave - at aktie penge i to grupper (ikke nødvendigvis lige store), som hver er det samme antal mønter op haler.
Se svaret.
Skjul.
Opdele mønter i to grupper: én 40, den anden 10. Drej nu alle de penge fra den anden gruppe. Voila kan omfatte lys: opgaven er fuldført. Tro ikke mig - check.
For pedanter matematikere forklare algoritmen. Efter den blinde adskillelse i to grupper her er hvad der skete: den første venstrefløjens haler; og andet henholdsvis - (10 - x) haler (for i alt 10 betingelser tails problem). A eagles dermed - 10 - (10 - x) = x. Det vil sige, at antallet af ørne i den anden gruppe er antallet af haler i den første.
Gør enkel trin - slå over alle de mønter i den anden flok. Således alle mønt-Eagles (enheder) er mønter-haler, og deres antal er det samme som antallet af haler i den første gruppe.
7. Hvordan man ikke at blive gift
Når ejeren af små butikker i Italien skylder en stor sum til moneylender. Muligheden for at tilbagebetale en gæld, han ikke gjorde. Men der var en smuk datter, der længe har elsket långiveren.
- Lad os gøre det, - har tilbudt købmanden moneylender. - Du vydaosh datter til mig, og jeg husker som en relation af pligt. Nå, på hænderne?
Men pigen ønskede ikke at gifte sig en gammel og grim mand. Derfor butiksindehaveren nægtede. Men en potentiel søn bifangst i stemmen gynger og lavet et nyt forslag.
- Jeg ønsker ikke at tvinge nogen - sagde ågerkarlen sagte. - Lad os alle til at løse sagen. Se, jeg vil sætte i posen to sten - sort og hvid. Og lad min datter uden at kigge trækker ud en af dem. Hvis det er sort, havde vi gift, og jeg tilgiver dig gælden. Hvis Hvid - jeg tilgiver gælden bare sådan, uden at skulle aflevere din datter.
Handlen syntes retfærdig, og denne gang min far aftalt. Pengeudlåner bøjede sig over på sporet strøet med grus, hurtigt samlet op stenene og læg dem i en pose. Men datteren så en forfærdelig ting: de to var sorte småsten! Uanset hvad det er trukket ud, ville hun nødt til at gifte sig. Selvfølgelig var det muligt at eksponere moneylender i bedrag, idet begge dele på samme sten. Men der kunne komme ind i et raseri og annullere transaktionen ved at anmode om en gæld fuldt ud.
Efter at tænke i et par sekunder, hun trygt rakte sin hånd til posen. Og jeg gjorde noget, der reddede hendes far fra gæld, og det selv - behovet for ægteskab. Retfærdighed erkendte pengeudlåner selv hendes handling. Hvad gjorde hun?
Se svaret.
Skjul.
Hun trak en sten, og uden at skulle vise nogen, hvis et uheld faldt det på sporet. Sten derefter blandet med resten af småsten.
- Åh, jeg er så klodset! - foldede hænder butiksindehaveren datter. - Men det er ikke noget. Efter alt, kan vi se i posen. Hvis der var en hvid sten, så jeg trak den sorte. Og omvendt.
Selvfølgelig, når alle kiggede i posen, der blev opdaget en sort sten. Selv pengeudlåner Jeg var nødt til at blive enige: det betyder, at pigen trak den hvide. Og hvis ja - brylluppet ikke vil være, og er nødt til at tilgive gælden.
8. Du har forvekslet koden ...
Du lukkede kufferten på en digital lås med trecifret kode numre og ved et uheld glemt. men hukommelse Det giver følgende tips:
- 682 - denne kode er et af tallene er korrekt og er på sin plads;
- 614 - et af tallene rette, men bør ikke på plads;
- 206 - korrekte to cifre, men de to er ikke på plads;
- 738 - alt nonsens, ingen hit;
- 870 - Et tal er korrekt, men ikke på sin plads.
Disse oplysninger er nok til at finde den rigtige kode. Hvad er det?
Se svaret.
Skjul.
042.
Efter den fjerde spids, krydse ud af alle de kombinationer af tallene 7, 3 og 8 - de er i den ønskede kode er bestemt ikke. Vi finder ud fra den første antydning af, at hans plads er enten 6 eller 2. Men hvis det er 6, er det ikke tilstanden af den anden anelse om, hvor 6 står i begyndelsen. Så det sidste ciffer i koden - 2. A6 er fraværende i Cipher.
Fra den tredje fingerpeg vi konkludere, at de rigtige numre af koden - 2 og 0. I dette tilfælde 2 er i bunden. Det betyder, at 0 - på jorden. Således bliver vi opmærksomme på de første og tredje cifre i koden: 0... 2.
Er i forhold til andet fingerpeg. Figur 6 lavvandede før. Enheden passer ikke: det er kendt, at det ikke er på sin plads, men alle de mulige placeringer for det - første og sidste - er allerede besat. Således er den sande tal er kun 4. Det og flytte ind i midten af den resulterende kode - 042.
9. Sådan deler kagen
Og endelig, lidt sød. Har du fået torteHvilket skal divideres med antallet af gæster - 8 stk. Det eneste problem er, at det skal gøres, efter at have gjort blot tre nedskæringer. Til højre?
Se svaret.
Skjul.
Lav to snit på tværs - som hvis du ønsker at dele kagen i fire lige store dele. En tredje indsnit swipe ikke lodret men vandret langs skillelinjen behandler.

se også🔎🤓✌️
- 10 opgaver på logik og intelligens
- 4 forklare hovedkortet af loven om de simple eksempler
- 5 effektive værktøjer til udvikling af kreativitet
- Løs 3 puslespil trick og finde ud af hvor klog du er
- 10 tricky opgaver til test logik og Vid

